Difference between revisions of "Initialisation"
From Adaptive Population based Simplex
(→Basic initialisation (i0)) |
(→Population cost) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 5: | Line 5: | ||
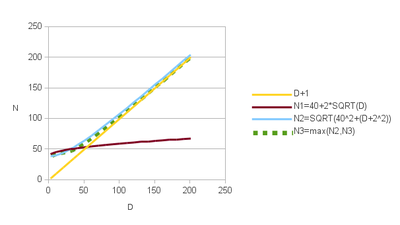
$N=\max\left(40+2\sqrt{D},\sqrt{40^{2}+\left(D+2\right)^{2}}\right)\label{eq:N_popsize}$ | $N=\max\left(40+2\sqrt{D},\sqrt{40^{2}+\left(D+2\right)^{2}}\right)\label{eq:N_popsize}$ | ||
| − | where $D$ is the dimension of the search space. Note that $N$ needs to be at least equal to $D+ | + | where $D$ is the dimension of the search space. Note that $N$ needs to be at least equal to $D+1$. |
We will need the volume $V(0)$ of the previous simplex. As no one has been defined yet, we simply set it to 0:<br /> | We will need the volume $V(0)$ of the previous simplex. As no one has been defined yet, we simply set it to 0:<br /> | ||
| Line 11: | Line 11: | ||
=== Population cost === | === Population cost === | ||
| − | Evaluate the $N$ individuals. Save the best one as $Best$. | + | Evaluate the $N$ individuals, thanks to the function $f$ we are studying. Save the best one as $Best$. |
The sum of all values (they are all supposed to be positive, which is always possible), is the initial ''population cost'' $C$. We are trying here to minimise it. | The sum of all values (they are all supposed to be positive, which is always possible), is the initial ''population cost'' $C$. We are trying here to minimise it. | ||
Latest revision as of 17:55, 28 June 2013
Basic initialisation (i0)
Draw at random $N$ agents (positions) in the search space, according to an uniform distribution.
$N=\max\left(40+2\sqrt{D},\sqrt{40^{2}+\left(D+2\right)^{2}}\right)\tag{1}$
where $D$ is the dimension of the search space. Note that $N$ needs to be at least equal to $D+1$.
We will need the volume $V(0)$ of the previous simplex. As no one has been defined yet, we simply set it to 0:
$$V(0)=0$$
Population cost
Evaluate the $N$ individuals, thanks to the function $f$ we are studying. Save the best one as $Best$.
The sum of all values (they are all supposed to be positive, which is always possible), is the initial population cost $C$. We are trying here to minimise it.