Difference between revisions of "Presentation"
From Adaptive Population based Simplex
| Line 14: | Line 14: | ||
APS has been inspired by some previous works, in particular the ones of Luo et al. <ref name=luo2012lowdimensional> Luo, C. & Yu, B. Low dimensional simplex evolution: a new heuristic for global optimization Journal of Global Optimization, 2012, 52, 45-55</ref> <ref name=luo_modifications_2013>Luo, C.; Zhang, S.-L. & Yu, B. Some modifications of low-dimensional simplex evolution and their convergence Optimization Methods and Software, 2013, 28, 54-81 </ref> on Low dimensional simplex evolution (LDSE). | APS has been inspired by some previous works, in particular the ones of Luo et al. <ref name=luo2012lowdimensional> Luo, C. & Yu, B. Low dimensional simplex evolution: a new heuristic for global optimization Journal of Global Optimization, 2012, 52, 45-55</ref> <ref name=luo_modifications_2013>Luo, C.; Zhang, S.-L. & Yu, B. Some modifications of low-dimensional simplex evolution and their convergence Optimization Methods and Software, 2013, 28, 54-81 </ref> on Low dimensional simplex evolution (LDSE). | ||
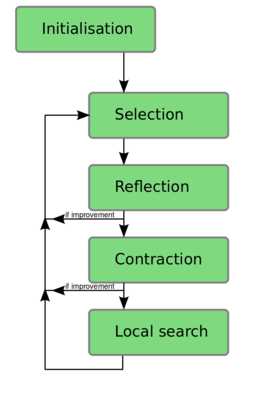
| − | Each phase is explained on its own page (just click on the corresponding area of the figure). After the initialisation of N individuals, all the other phases are in a loop on them. In the explanation, the current individual is called xi. This loop is | + | Each phase is explained on its own page (just click on the corresponding area of the figure). After the initialisation of N individuals, all the other phases are in a loop on them. In the explanation, the current individual is called xi. This loop is repeated as long as a stop criterion is not met. As usually, the stop criterion is either a maximum number of fitness evaluations, or an error value found smaller than a predefined threshold. |
<references/> | <references/> | ||
Latest revision as of 10:21, 23 June 2014
APS has been inspired by some previous works, in particular the ones of Luo et al. [1] [2] on Low dimensional simplex evolution (LDSE).
Each phase is explained on its own page (just click on the corresponding area of the figure). After the initialisation of N individuals, all the other phases are in a loop on them. In the explanation, the current individual is called xi. This loop is repeated as long as a stop criterion is not met. As usually, the stop criterion is either a maximum number of fitness evaluations, or an error value found smaller than a predefined threshold.
- Jump up ↑ Luo, C. & Yu, B. Low dimensional simplex evolution: a new heuristic for global optimization Journal of Global Optimization, 2012, 52, 45-55
- Jump up ↑ Luo, C.; Zhang, S.-L. & Yu, B. Some modifications of low-dimensional simplex evolution and their convergence Optimization Methods and Software, 2013, 28, 54-81