Difference between revisions of "Initialisation"
From Adaptive Population based Simplex
(→Basic method) |
(→Population cost) |
||
| (7 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | == Basic initialisation (i0) == | |
| + | [[Image:Basic APS N vs D.png|right|thumb|400px|Population size vs Dimension]] | ||
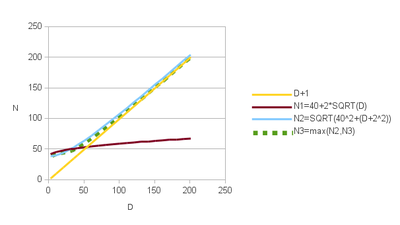
| + | Draw at random N agents (positions) in the search space, according to an uniform distribution. | ||
| + | N=max | ||
| − | + | where D is the dimension of the search space. Note that N needs to be at least equal to D+1. | |
| − | + | We will need the volume $V(0)$ of the previous simplex. As no one has been defined yet, we simply set it to 0:<br /> | |
| + | V(0)=0 | ||
| − | $N | + | === Population cost === |
| + | Evaluate the $N$ individuals, thanks to the function f we are studying. Save the best one as $Best$. | ||
| − | + | The sum of all values (they are all supposed to be positive, which is always possible), is the initial ''population cost'' C. We are trying here to minimise it. | |
Latest revision as of 18:55, 28 June 2013
Basic initialisation (i0)
Draw at random N agents (positions) in the search space, according to an uniform distribution.
N=\max\left(40+2\sqrt{D},\sqrt{40^{2}+\left(D+2\right)^{2}}\right)\tag{1}
where D is the dimension of the search space. Note that N needs to be at least equal to D+1.
We will need the volume V(0) of the previous simplex. As no one has been defined yet, we simply set it to 0:
V(0)=0
Population cost
Evaluate the N individuals, thanks to the function f we are studying. Save the best one as Best.
The sum of all values (they are all supposed to be positive, which is always possible), is the initial population cost C. We are trying here to minimise it.