Initialisation
From Adaptive Population based Simplex
Basic initialisation (i0)
Draw at random $N$ agents (positions) in the search space, according to an uniform distribution.
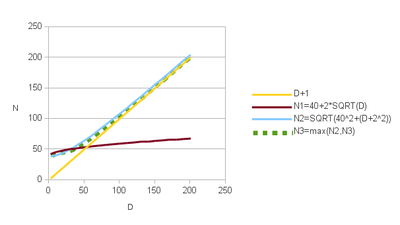
$N=\max\left(40+2\sqrt{D},\sqrt{40^{2}+\left(D+2\right)^{2}}\right)\tag{1}$
where $D$ is the dimension of the search space. Note that $N$ needs to be at least equal to $D+1$.
We will need the volume $V(0)$ of the previous simplex. As no one has been defined yet, we simply set it to 0:
$$V(0)=0$$
Population cost
Evaluate the $N$ individuals. Save the best one as $Best$.
The sum of all values (they are all supposed to be positive, which is always possible), is the initial population cost $C$. We are trying here to minimise it.